DeltaNet Explained (Part I)

A gentle and comprehensive introduction to the DeltaNet

This blog post series accompanies our NeurIPS ‘24 paper - Parallelizing Linear Transformers with the Delta Rule over Sequence Length (w/ Bailin Wang, Yu Zhang, Yikang Shen and Yoon Kim). You can find the implementation here and the presentation slides here.

  1. Part I - The Model
  2. Part II - The Algorithm
  3. Part III - The Neural Architecture

Linear attention as RNN

Notations: we use CAPITAL BOLD letters to represent matrices, lowercase bold letters to represent vectors, and regular lowercase letters to represent scalars.

What is linear attention?

The vanilla softmax attention mechanism, though powerful, suffers from quadratic complexity in sequence length. Let’s see how linear attention addresses this issue by starting with the standard softmax attention (assuming single head):

\[\begin{aligned} \mathrm{Parallel\ training:} &&& \mathbf{O} = \mathrm{softmax}(\mathbf{Q}\mathbf{K}^\top \odot \mathbf{M})\mathbf{V} &&\in \mathbb{R}^{L\times d} \\ \mathrm{Iterative\ inference:} &&&\mathbf{o_t} = \sum_{j=1}^t \frac{\exp(\mathbf{q}_t^\top \mathbf{k}_j)}{\sum_{l=1}^t\exp(\mathbf{q}^\top_t \mathbf{k}_l)}\mathbf{v}_j &&\in \mathbb{R}^d \end{aligned}\]

Here,

What linear attention does is to simply remove the softmax operator The original linear attention formulation incorporates feature mapping on queries and keys along with a normalizer term, but recent studies suggest these components may not be essential..:

\[\begin{aligned} \mathrm{Parallel\ training：} &&&\mathbf{O}= (\mathbf{Q}\mathbf{K}^\top \odot \mathbf{M})\mathbf{V} &&\in \mathbb{R}^{L\times d} \\ \mathrm{Iterative\ inference：}&&&\mathbf{o_t} = \sum_{j=1}^t (\mathbf{q}_t^\top \mathbf{k}_j) \mathbf{v}_j &&\in \mathbb{R}^d \end{aligned}\]

While removing softmax alone doesn’t immediately reduce computational complexity, it enables a crucial mathematical property: linearity. This property, particularly associativity, allows us to restructure the computations in ways that significantly improve efficiency. For training, researchers have developed chunkwise parallel techniques that leverage this linearity to achieve subquadratic complexity while maintaining hardware efficiency, which forms the foundation of our open-source flash-linear-attention library.

For inference, we can also rearrange the computation as follows:

\(\begin{aligned} &&&&\mathbf{o_t} = \sum_{j=1}^t \mathbf{v}_j(\mathbf{k}_j^\top \mathbf{q}_t) &&&&& \mathbf{k}_j^\top \mathbf{q}_t = \mathbf{q}_t^\top \mathbf{k}_j \in \mathbb{R}\\ &&&&= (\sum_{j=1}^t\mathbf{v}_j\mathbf{k}_j^\top)\mathbf{q}_t &&&&&\text{By associativity} \end{aligned}\) $$

Let’s define a state matrix \(\mathbf{S}_t = \sum_{j=1}^t\mathbf{v}_j\mathbf{k}_j^\top\). Then the computation can be expressed as:

\[\mathbf{S}_t = \mathbf{S}_{t-1} + \mathbf{v}_t\mathbf{k}_t^\top \in \mathbb{R}^{d\times d}, \quad \mathbf{o}_t = \mathbf{S}_t \mathbf{q}_t \in \mathbb{R}^{d}\]

This formulation reveals that linear attention is essentially a linear RNN with a matrix-valued state \(\mathbf{S}\) that accumulates key-value outer products, enabling efficient state (size) expansion from \(\mathcal{O}(d)\) to \(\mathcal{O}(d^2)\).

Why do we want state expansion? Traditionally, RNN's hidden dimension is often the same (or of the same magnitude) as the input dimension, due to the expensive matrix-multiply-based state update. However, RNN solely relies on the recurrent state to remember the entire history and state size tends to be the bottleneck to remember sufficient amount of information, especially in retrieval tasks. We've been observing a substantial amount of research investigating hardware-efficient state expansion since Mamba1 explicitly pointed it out, and linear attention styled outer-product-based update has proven to be optimal in terms of efficiently scaling state up (Mamba2 also adopts this strategy!). In our previous HGRN2 work, we investigated different approaches for state expansion, and the outer product based mechanism has proven to be both performant and scalable.

With this approach, we only need to store and update \(\mathbf{S}_t\) instead of maintaining all previous key-value pairs. This optimization dramatically improves efficiency: the time complexity for autoregressive inference reduces from \(\mathcal{O}(L^2d)\) to \(\mathcal{O}(Ld^2)\), while the space complexity improves from \(\mathcal{O}(Ld)\) to \(\mathcal{O}(d^2)\). These improvements make this method particularly advantageous in two scenarios:

No Free Lunch: Key Limitations of Linear Attention

Unfortunately, there is no free lunch. The fixed-size state matrix in linear attention means it cannot perfectly preserve all historical information, making exact retrieval particularly challenging.

More formally, linear attention implements a key-value associative memory, which is the sum of outer products between keys and values \(\mathbf{S} = \sum \mathbf{v}_i\mathbf{k}_i^\top\). Assuming all keys are normalized to unit length, when we try to retrieve a value associated with a specific key \(k_j\), we get:

\[\begin{aligned} \mathbf{S}\mathbf{k}_j &= \sum \mathbf{v}_i (\mathbf{k}_i^\top \mathbf{k}_j) \\ &= \mathbf{v}_j + \underbrace{\sum_{i\neq j} (\mathbf{k}_i^\top \mathbf{k}_j)\mathbf{v}_i}_{\text{retrieval error}} \end{aligned}\]

To minimize the retrieval error term, we need \(\mathbf{k}_i^\top \mathbf{k}_j = 0\) for all \(i\neq j\) - in other words, all keys should be orthogonal to each other. However, this reveals a fundamental limitation: in a \(d\)-dimensional space, you can only have at most \(d\) orthogonal vectors. This explains why increasing head dimension helps (For example, Sun et al. have demonstrated the necessity of increasing head dimensions to enhance model performance) - it provides more “room” in the vector space for storing distinct key-value pairs!

This theoretical limitation manifests in practice: vanilla linear attention has underperformed compared to softmax attention (by a large margin) in language modeling. The primary cause is memory “overload”: in this key-value associative memory system, we can only add new key-value associations without the ability to erase existing information. As sequences grow longer, this leads to accumulating “retrieval errors” that degrade performance. Indeed, as noted by David Eagleman in his book “Livewired: The Inside Story of the Ever-Changing Brain”,

“The enemy of memory is not time; it’s other memories.”

(Thanks to Kazuki Irie for the reference!). Recent advances in gated variants of linear attention (such as GLA and Mamba) have significantly narrowed the performance gap with standard attention in language modeling tasks by incorporating a forgetting mechanism. However, these models still face fundamental challenges with in-context retrieval and exact copying capabilities—limitations that have been both empirically observed and theoretically proven in recent work.

Click here to learn more about gated variants of linear attention Given the close relationship between linear attention and RNN, it is no wonder that researchers want to enhance linear attention with the (forgetting) gating mechanisms, which has been shown unreasonably effective in nonlinear RNN and linear RNN:

\[\mathbf{S}_t = \mathbf{G}_t \odot \mathbf{S}_{t-1} + \mathbf{v}_t\mathbf{k}_t^\top\]

with different structured parameterization for \(\mathbf{G}_t \in \mathbb{R}^{d\times d}\) for parameter efficiency, often with outer product structure. Different models have proposed various ways to structure this gating matrix:

For Decaying Fast weight: \[\mathbf{G}_t = \mathbf{\beta_t} \mathbf{\alpha_t}^\top\]

For GLA: \[\mathbf{G}_t = \mathbf{1} \mathbf{\alpha_t}^\top\]

For Mamba1: \[\mathbf{G}_t = \exp(-(\mathbf{\Delta_t} \mathbf{1}^\top) \odot \exp(A))\]

For Mamba2: \[\mathbf{G}_t = \gamma_t \mathbf{1}\mathbf{1}^\top\]

Cf. Table 1 of GLA for a summarization.

DeltaNet: Linear Attention with Delta Rule

What is Delta Rule?

The Delta Rule is a fundamental error-correction learning principle in neural networks. Its core idea is beautifully simple: adjust the model’s parameters based on the difference (delta) between what we want (target) and what we actually get (prediction).

To understand this intuitively, imagine teaching a child to aim at a target. If they shoot too far to the left, you’d tell them to adjust right; too far right, adjust left. The size of the adjustment depends on how far they missed - a concept directly reflected in the Delta Rule.

Click to expand Delta Rule code 
import numpy as np

def delta_rule(x, y, epochs=100, lr=0.1):
    """
    Simple delta rule implementation
    x: input features (N samples by D features)
    y: target values (N samples)
    """
    # Initialize weights
    w = np.zeros(x.shape[1])
    
    # Train
    for _ in range(epochs):
        for i in range(len(x)):
            # Forward pass
            pred = np.dot(x[i], w)
            
            # Compute error
            error = y[i] - pred
            
            # Update weights
            w += lr * error * x[i]
            
    return w

# Example usage
if __name__ == "__main__":
    # Generate toy data
    x = np.random.randn(100, 3)  # 100 samples, 3 features
    true_w = np.array([0.5, -0.2, 0.1])
    y = np.dot(x, true_w) + 0.1 * np.random.randn(100)
    
    # Train
    w = delta_rule(x, y)
    print("True weights:", true_w)
    print("Learned weights:", w)

What is DeltaNet?

DeltaNet applies this error-correction principle to linear attention. Instead of simply accumulating key-value outer product, it updates its state based on prediction errors:

\[\begin{align*} \mathbf{S}_{t} &= \mathbf{S}_{t-1} - \beta_t(\mathbf{S}_{t-1} \mathbf{k}_t - \mathbf{v}_t)\mathbf{k}_t^\top \\ &= \mathbf{S}_{t-1} - \beta_t \mathbf{S}_{t-1} \mathbf{k}_t \mathbf{k}_t^\top + \beta_t \mathbf{v}_t \mathbf{k}_t^\top \end{align*}\]

The parallel to the Delta Rule becomes clear when we break down the components:

We will revisit this form later, showing how it can emerge naturally from a single gradient descent step on a (online) loss function.

There’s another intuitive way to understand this update rule. Think of \(\mathbf{S}_{t-1}\mathbf{k}_t\) as retrieving the “old value” associated with the current key \(\mathbf{k}_t\) from memory. When we encounter a newly associated value \(\mathbf{v}_t\) for the same key, rather than blindly overwriting, we make a careful update:

\[\begin{align*} \mathbf{v}_t^{\text{new}} &= (1-\beta_t) \mathbf{v}_t^{\text{old}} + \beta_t \mathbf{v}_t, \\ \mathbf{S}_t &= \mathbf{S}_{t-1} - \underbrace{\mathbf{v}_t^{\text{old}} \mathbf{k}_t^\top}_{\text{erase}} + \underbrace{\mathbf{v}_t^{\text{new}} \mathbf{k}_t^\top}_{\text{write}} \end{align*}\]

where \(\mathbf{v}_t^{\text{new}}\) is a learned combination of the old and current values, controlled by a dynamic \(\beta_t \in (0,1)\): when \(\beta_t=0\), the memory content remains intact, and when \(\beta_t=1\), we completely replace the old associated value with the new one.

DeltaNet as a Strong In-context Learning RNN

MQAR (Multi-Query Associative Recall) is a recent popular synthetic benchmark aimed at measuring the in-context associative recall ability for subquadratic models.

The MQAR task works as follows: Each letter is associated with a number, and the model is asked to correctly recall the number associated with each letter in a query sequence.

For example, given the input:

A 4 B 3 C 6 F 1 E 2 → A ? C ? F ? E ? B ?

The format consists of:

  1. Key-Value pairs (before the arrow): Letters paired with their corresponding numbers
  2. Query sequence (after the arrow): Letters whose associated numbers need to be recalled

The correct output for this example would be:

4, 6, 1, 2, 3

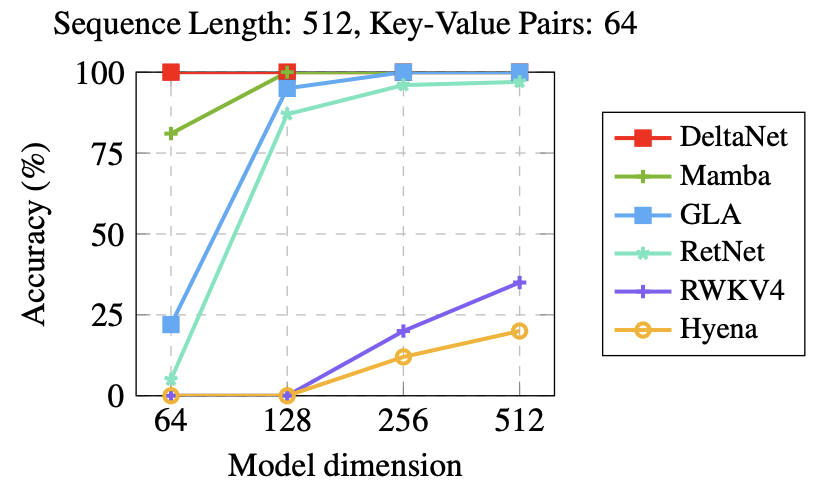
While conventional gated convolution and recurrent models generally underperform in this task, in our experiments, we show that DeltaNet Interestingly, DeltaNet was initially designed to improve associative recall performance but remained largely overlooked until this work. demonstrates notably strong performance:

The hardest setting from the original Zoology paper

This initial success was particularly exciting—achieving perfect performance on MQAR exceeded our expectations. What makes this result especially promising is that MQAR performance strongly correlates with “Associative-Recall-Hit” in real-world language modeling tasks. Associative recall failures are a primary source of errors in subquadratic models and largely account for their perplexity gap relative to softmax attention. Thus, DeltaNet’s perfect MQAR performance suggested significant potential.

We’ve also conducted experiments on MAD, another more comprehensive benchmark than MQAR that is also motivated to test new architecture’s capacities, and the results are summarized below:

Model Compress Fuzzy Recall In-Context Recall Memorize Noisy Recall Selective Copy Average
Transformer 51.6 29.8 94.1 85.2 86.8 99.6 74.5
Hyena 45.2 7.9 81.7 89.5 78.8 93.1 66.0
Multihead Hyena 44.8 14.4 99.0 89.4 98.6 93.0 73.2
Mamba 52.7 6.7 90.4 89.5 90.1 86.3 69.3
GLA 38.8 6.9 80.8 63.3 81.6 88.6 60.0
DeltaNet 42.2 35.7 100 52.8 100 100 71.8

where DeltaNet demonstrates its strong in-context recall capacities. These synthetic tasks are inexpensive to run and offer clear evidence that DeltaNet is likely to perform well at scale. This motivated us to focus on developing DeltaNet’s training algorithm and kernel implementation—after all, scaling up an arbitrary architecture without demonstrating its potential would risk wasting significant time and resources.

In the next post, we’ll explore a beautiful algorithm that parallelizes DeltaNet across sequence length. But first, let’s build some intuition about why DeltaNet is particularly well-suited for in-context retrieval tasks.

Why is DeltaNet Superior at In-context Retrieval Compared to Linear Attention?

DeltaNet’s update rule can be derived by sequentially minimizing the mean squared error (MSE) between the desired output and the predicted output at each time step \(t\) using gradient descent: This formulation reveals an interesting connection to Test-Time-Training (TTT) : DeltaNet becomes mathematically equivalent to TTT-linear under two specific conditions: (1) when nonlinear components such as layer normalization are removed, and (2) when the mini-batch size in TTT is set to one.

\[\mathcal{L}_t(\mathbf{S}) = \frac{1}{2}\|\mathbf{S} \mathbf{k}_t - \mathbf{v}_t\|^2\]

Applying gradient descent to minimize this MSE loss gives:

\[\begin{aligned} \mathbf{S}_t &= \mathbf{S}_{t-1} - \eta_t \nabla \mathcal{L}_t(\mathbf{S}_{t-1}) \\ &= \mathbf{S}_{t-1} - \eta_t \left(\mathbf{S}_{t-1} \mathbf{k}_t - \mathbf{v}_t\right) \mathbf{k}_t^\top \end{aligned}\]

When the learning rate \(\eta_t\) is set to \(\beta_t\), this results in DeltaNet’s update rule.

In contrast, vanilla linear attention employs a linear loss function:

\[\mathcal{L}^\prime_t(\mathbf{S}) = -\langle \mathbf{S} \mathbf{k}_t, \mathbf{v}_t \rangle\]

The corresponding update rule for linear attention is:

\[\begin{aligned} \mathbf{S}_t &= \mathbf{S}_{t-1} - \eta_t \nabla \mathcal{L}_t^\prime(\mathbf{S}_{t-1}) \\ &= \mathbf{S}_{t-1} + \eta_t \mathbf{v}_t \mathbf{k}_t^\top \end{aligned}\]

By setting \(\eta_t = 1\), the standard linear attention update is recovered.

Thus, DeltaNet’s superior performance in in-context retrieval becomes evident—it minimizes MSE at each step, making it ideal for tasks like associative recall where reducing large errors is crucial for accurate retrieval.