DeltaNet Explained (Part III)

Modernize DeltaNet neural architecture

This blog post series accompanies our NeurIPS ‘24 paper - Parallelizing Linear Transformers with the Delta Rule over Sequence Length (w/ Bailin Wang, Yu Zhang, Yikang Shen and Yoon Kim). You can find the implementation here and the presentation slides here.

DeltaNet architecture design

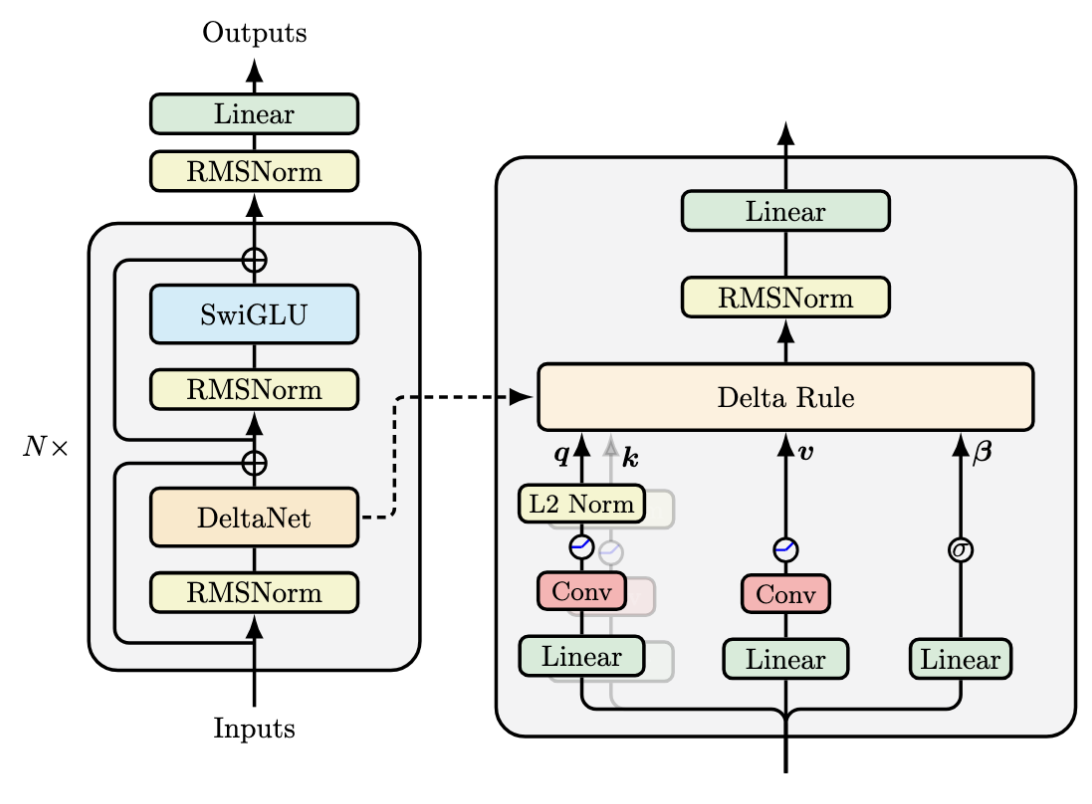
DeltaNet architecture

In this final post, we explore our modernization of DeltaNet’s architecture. While maintaining the core delta rule mechanism, we’ve introduced several architectural improvements that significantly enhance its performance.

At a high level, DeltaNet follows the modern transformer block design popularized by Llama, alternating between token mixing (DeltaNet replacing self-attention) and channel mixing (SwiGLU). Our main architectural modifications focus on the token mixing layer, where we introduce three key improvements. First, we replace the original L₁ normalization and 1+ELU activation with L₂ normalization and SiLU activation for query and key processing. Second, we add short convolution operations after the linear projections for queries, keys, and values. Third, we incorporate output normalization before the final projection.

The complete processing pipeline now follows this structure:

Query/Key: Linear → ShortConv → SiLU → L₂Norm
Value: Linear → ShortConv → SiLU
Beta: Linear → Sigmoid
Output: Delta rule(query, key, value, beta) → RMSNorm → Linear

Let’s examine why each of these modifications proves crucial for model performance.

Normalization on Queries and Keys

A crucial aspect of DeltaNet’s architecture is the normalization of key vectors. This isn’t just a technical detail - it’s fundamental to the model’s stability and effectiveness. Consider DeltaNet’s core equation:

\[\mathbf{S}_{t} = \mathbf{S}_{t-1} (\mathbf{I} - \beta_t \mathbf{k}_t\mathbf{k}_t^\top) + \mathbf{v}_t\mathbf{k}_t^\top\]

The stability of this recurrent system depends on the eigenvalues of its transition matrix \((\mathbf{I} - \beta_t \mathbf{k}_t\mathbf{k}_t^\top)\). This matrix has an elegant spectral structure:

The eigenvalue in the direction of \(\mathbf{k}_t\) is \(1 - \beta_t\|\mathbf{k}_t\|^2\)
All directions perpendicular to \(\mathbf{k}_t\) have eigenvalue 1

For stable updates, we need all eigenvalues to have magnitude \(\leq 1\). Given \(0 \leq \beta_t \leq 1\), this requires \(\|\mathbf{k}_t\|^2 \leq 2\). While the original DeltaNet used L₁ normalization, we found L₂ normalization offers both better empirical performance and a more intuitive geometric interpretation: when \(\beta_t = 1\) and \(\|\mathbf{k}_t\|_2 = 1\), the matrix \(\mathbf{I} - \mathbf{k}_t\mathbf{k}_t^\top\) becomes a projection matrix that selectively erases information in the direction of \(\mathbf{k}_t\) while preserving all other directions.

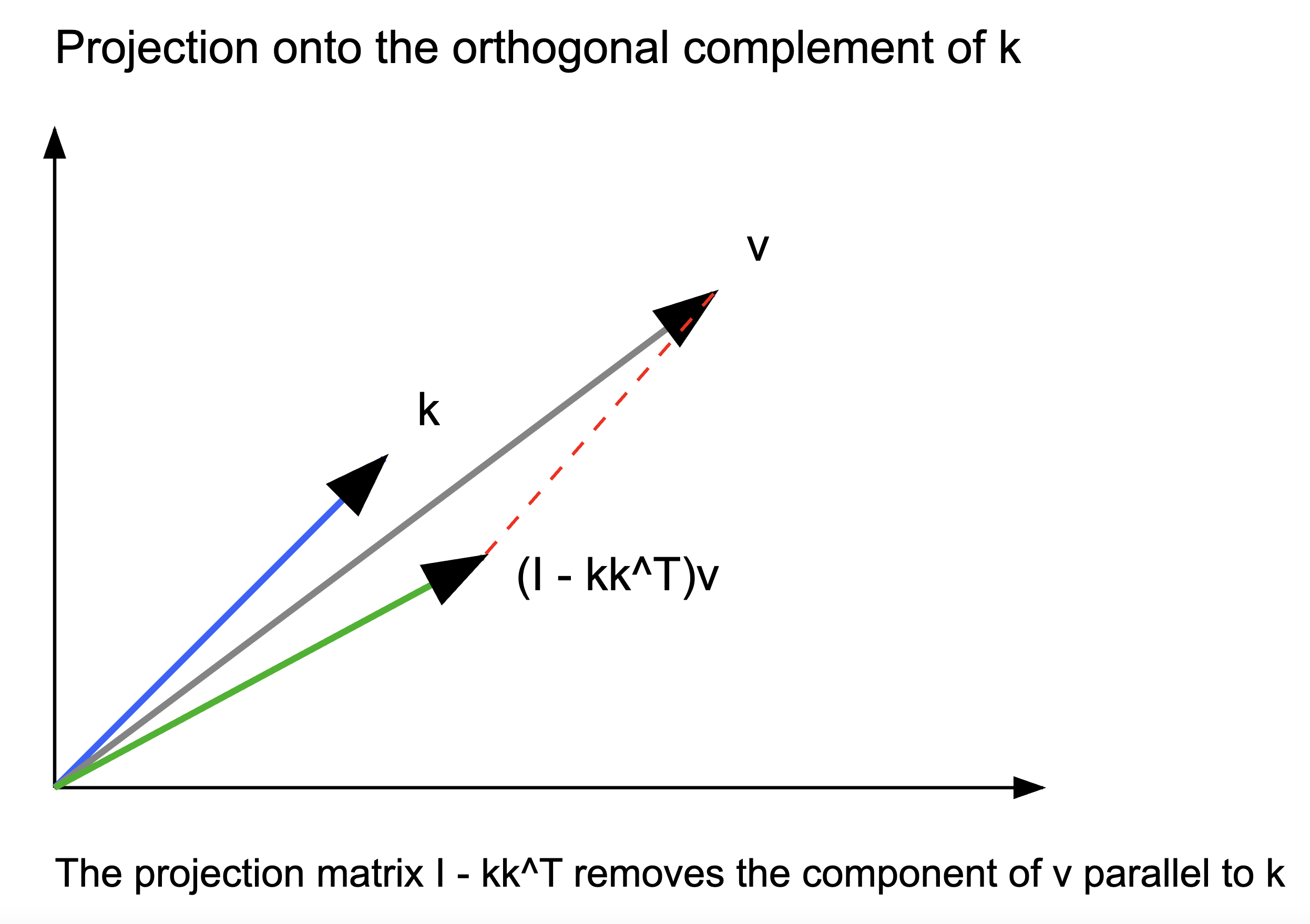
The projection matrix has an important geometric effect: when applied to any vector, it removes the component parallel to \(\mathbf{k}_t\) while preserving all orthogonal components. In the context of DeltaNet, this means each update “cleans up” the state by removing components that might interfere with the current key’s direction. This operation helps maintain cleaner separations between different key vectors over time, reducing the interference between stored patterns (or the retrieval error) that we discussed in the first post. This geometric property helps explain why L₂ normalization, which directly aligns with this projection interpretation, leads to better retrieval performance than L₁ normalization.

We also find that applying L₂ normalization to queries improves model performance. This observation aligns with recent trends in self-attention architectures, where QK-normalization has emerged as an effective technique for stabilizing and enhancing attention mechanisms.

Finally, we note a potential limitation in our current design: our transition matrices are constrained to have strictly positive eigenvalues. A recent insightful work demonstrates how this could limit the model’s state tracking capabilities. Fortunately, their proposed enhancement is remarkably simple - by adjusting our beta term to \(\beta_t = 2\beta_t\), we can allow for negative eigenvalues in our transition matrices. This one-line modification could meaningfully expand DeltaNet’s representational capabilities. We direct interested readers to the following discussion for a deeper analysis of this enhancement.

LLMs can now track states, finally matching this cat!
And we prove it.

But how? 🧵👇

1/ Paper: https://t.co/aKvrqYtkWh
with @julien_siems @jkhfranke @ZelaArber @FrankRHutter @MPontil pic.twitter.com/2OREoLkDyY
— Riccardo Grazzi ✈️ NeurIPS 2024 (@riccardograzzi) November 22, 2024

Normalization on Outputs

In standard linear attention, the output at each position is normalized by the sum of attention weights:

\[\mathbf{o}_t = \frac{(\sum_{i=1}^t \mathbf{v}_i \phi(\mathbf{k})_i^\top)\phi(\mathbf{q})_t}{\sum_{i=1}^t \phi(\mathbf{k})_i^\top \phi(\mathbf{q})_t}\]

where \(\phi\) is a positive feature map. However, a seminal analysis by Qin et al. demonstrates that this normalization term can lead to unbounded gradients and training instability. To address this issue, they propose removing the denominator and instead applying normalization to the output before the final projection. This architectural modification has since become standard practice, adopted by modern linear attention models including RetNet, GLA, Mamba2, and others.

Activation Function Choice

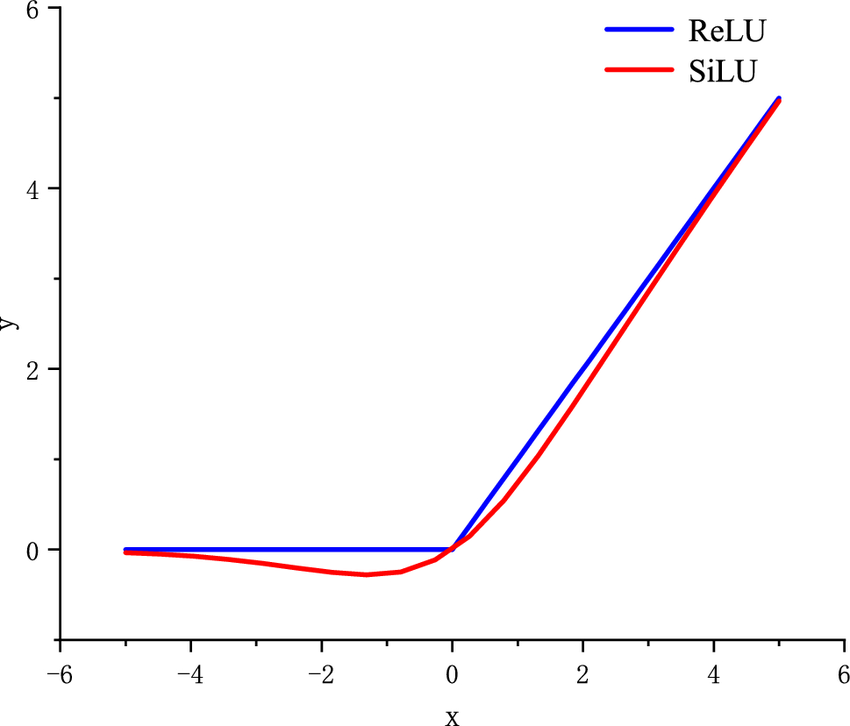
While the original DeltaNet used 1+ELU activation, our experiments show that SiLU activation provides better performance, a finding aligned with recent architectures like Mamba2, xLSTM, and LightningAttention . This presents an interesting contrast with traditional linear attention models, which typically choose activation functions that ensure positive attention scores through positive feature maps (e.g., ReLU, 1+ELU, exponential). The success of allowing negative values parallels findings from Differential Transformers , suggesting that restricting attention scores to be strictly positive may be unnecessarily limiting.

Short Convolution

Short convolution, i.e., depthwise separable Conv1D with small kernel window size as small as 4, has emerged as a crucial component in recent subquadratic attention models, appearing in various forms across architectures like Mamba, xLSTM, and MetaLA. This generalizes the previously proposed “shift-SSM” in H3 and has a close relationship to “token-shift” in RWKV.

While DeltaNet’s delta rule excels at content-based interactions, many linguistic patterns require precise positional information. Short convolution provides direct access to local context, enabling the model to capture position-dependent patterns without relying on content-based matching. This combination of content-based and position-sensitive processing has proven highly effective across modern architectures.

Experimental Results

With the parallel algorithm in hand, and with the architecture above, we are now ready to scale up DeltaNet to standard language modeling settings. Our evaluation spans three key metrics: language modeling (WikiText perplexity), common-sense reasoning (averaged across LAMBADA, PiQA, HellaSwag, WinoGrande, ARC-easy, and ARC-challenge), and in-context retrieval (averaged across FDA, SWDE, and SQuAD).

Regarding state size across architectures (H denotes number of layers, d denotes model dimension):

Architecture	State Expansion	Total State Size	Implementation Details
Mamba	16x	64Hd	Expands value projections to 2d and uses 16x expansion ratio; doubles effective state size by replacing FFN with Mamba layers
RetNet	512x	512Hd	Expands value projections to 2d; maintains fixed 256-dimensional query/key heads
GLA	256x	256Hd	Uses half-sized query/key heads relative to value heads; maintains 4d² parameters per layer
DeltaNet	128x	128Hd	Employs consistent 128-dimensional heads throughout the architecture

Main Results (340M+15B token)

Model	Wiki. ppl ↓	Avg. Common-sense ↑	Avg. Retrieval ↑	State Size
Transformer++	28.39	41.2	28.6	N/A
RetNet (w/o conv)	32.33	41.0	14.6	512x
Mamba (w. conv)	28.39	41.8	12.5	64x
GLA (w/o conv)	28.65	41.5	18.0	128x
DeltaNet (w. conv)	28.24	42.1	22.7	128x

DeltaNet achieves competitive performance across all metrics while maintaining reasonable state size requirements. Notably, it shows particular strength in retrieval tasks, supporting our hypothesis that its delta rule mechanism provides effective in-context retrieval capabilities.

Ablation Study (340M+15B token)

Model	Wiki. ppl ↓	Common-sense ↑	Retrieval ↑
DeltaNet (full)	28.24	42.1	22.7
- w/o short conv	29.08	41.4	18.6
- w. \(L_1\)-norm + 1+ELU	31.12	40.1	11.5
- w. \(L_2\)-norm + 1+ELU	28.03	42.1	21.8
- w. \(L_2\)-norm + ReLU	28.75	40.9	21.0

Our ablation studies highlight several important findings about DeltaNet’s architecture. Most significantly, retrieval performance shows strong sensitivity to the choice of normalization - \(L_2\) normalization substantially outperforms \(L_1\) normalization, supporting our theoretical analysis about projection properties. Short convolution also emerges as a crucial component, demonstrating that effective position-based addressing meaningfully complements DeltaNet’s content-based mechanism for retrieval tasks. The choice of activation function, while still relevant, shows more modest effects; SiLU provides incremental improvements over ReLU and 1+ELU, but its impact is less pronounced than either normalization or short convolution.

Hybrid Models: Combining DeltaNet with Attention

Left: Hybrid sliding window attention and DeltaNet model. Right: Hybrid global attention and DeltaNet model.

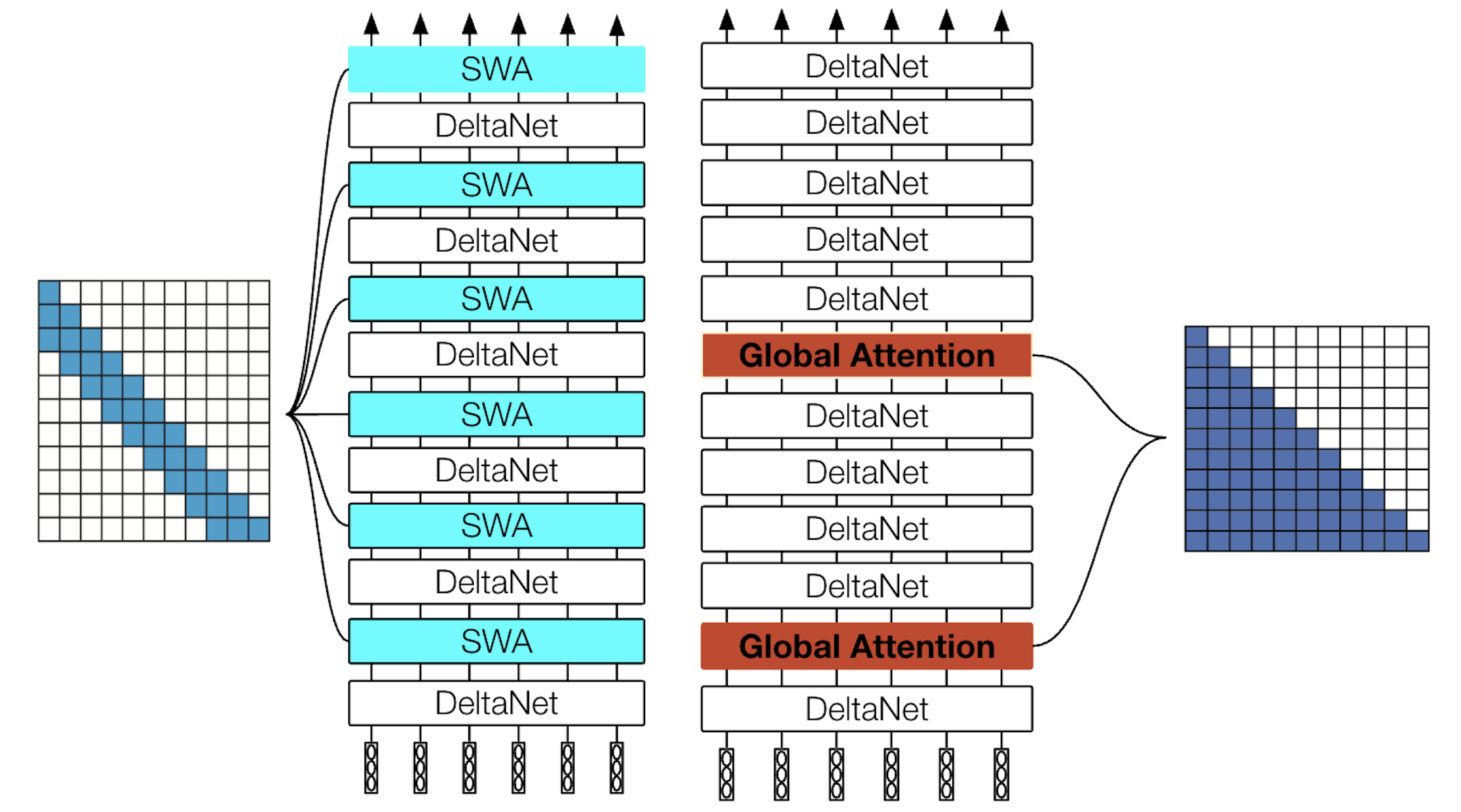
While DeltaNet’s delta rule mechanism shows promise for retrieval tasks, it still faces a fundamental limitation common to all RNN architectures: fixed state size. This constraint creates an inherent ceiling for retrieval performance, regardless of the choice of update rule. To overcome this limitation, we explore hybrid architectures that strategically combine DeltaNet with attention mechanisms.

Our first approach integrates sliding window attention with DeltaNet in an interleaving pattern, following recent architectures like Griffin and Samba. While this hybrid maintains subquadratic complexity due to the fixed window size, it inherits similar theoretical constraints as pure RNN models. As demonstrated in Griffin, the fixed context window can limit the retrieval of information beyond its scope.

This limitation led us to our second approach: augmenting DeltaNet with global attention. Rather than replacing many DeltaNet layers with attention, which would significantly impact inference efficiency, we choose to place just two global attention layers - one in the second layer and another at layer N/2-1, following H3. Though this technically makes the model no longer subquadratic, the sparing use of attention layers substantially reduces KV cache requirements compared to full Transformer models.

Results at the 340M parameter scale demonstrate the effectiveness of these hybrid approaches:

Model	Wiki. ppl ↓	Avg. Common-sense ↑	Avg. Retrieval ↑
Transformer++	28.39	41.2	28.6
DeltaNet	28.24	42.1	22.7
+ Sliding Attn	27.06	42.1	30.2
+ Global Attn	27.51	42.1	32.7

We then scaled our experiments to 1.3B parameters, training for 100B tokens on SlimPajama. The results reinforce our findings:

Model	Wiki. ppl ↓	Avg. Common-sense ↑	Avg. Retrieval ↑
Transformer++	16.85	50.9	41.8
DeltaNet	16.87	51.6	34.7
+ Sliding Attn	16.56	52.1	39.6
+ Global Attn	16.55	51.8	47.9

While sliding window attention provides substantial gains, it cannot fully match Transformer-level retrieval performance in larger scale. However, the addition of just two global attention layersRecent work demonstrates that using global attention in only a small portion (~10%) of total layers can be highly effective for model performance . yields remarkable results, surpassing even the Transformer baseline in retrieval tasks.

Finally, we evaluated a 3B parameter model trained on 1T tokens following the PowerLM-3B setup . These results place DeltaNet as a strong performer among RNN architectures while slightly trailing transformer-based models:

Model	ARC	HellaSwag	OBQA	PIQA	WinoGrande	MMLU	Average
Llama-3.2-3B	59.1	73.6	43.4	77.5	69.2	54.1	62.8
PowerLM-3B	60.5	74.6	43.6	79.9	70.0	45.0	62.3
DeltaNet-3B	60.4	72.8	41.0	78.5	65.7	40.7	59.8
RecurrentGemma-2B	57.0	71.1	42.0	78.2	67.6	31.8	57.9
RWKV-6-3B	49.5	68.6	40.6	76.8	65.4	28.4	54.9
Mamba-2.7B	50.3	65.3	39.4	75.8	63.1	26.1	53.3

The results demonstrate DeltaNet’s effectiveness across scales, though there remains a small gap compared to transformer architectures at larger sizes. We are currently exploring larger hybrid models combining DeltaNet with attention mechanisms - stay tuned for updates!